Carbon nanocones are conical
structures with linear dimensions of the order of one micrometer or less
in at least one direction.
The values of the base and height of the nanocones are of the same
order, which allows to separate them in a specific class,
featuring from sealed nanowires, which have a similar geometry but their
length is several orders of magnitude greater than the transverse
dimensions.
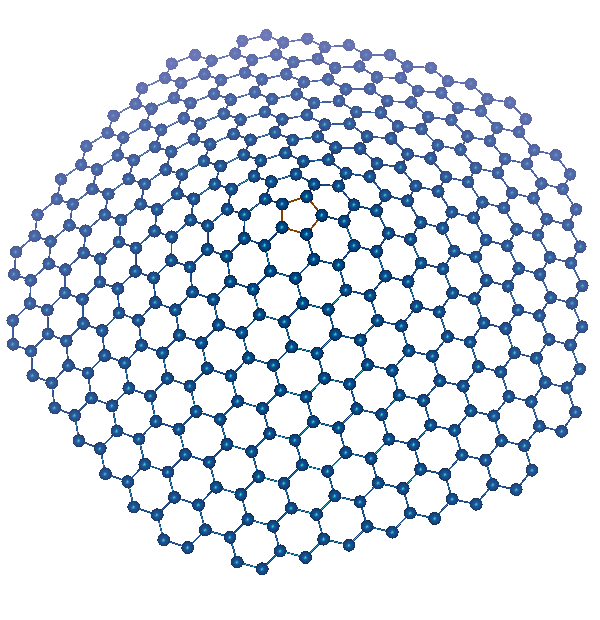
Nanocones can be both hollow and filled. Hollow nanocones can be
represented as a folded in a certain way sheet of graphene.
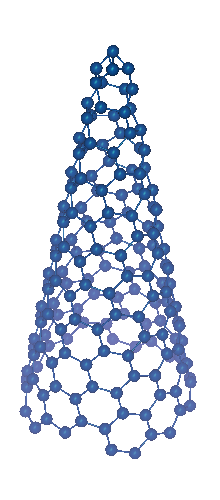
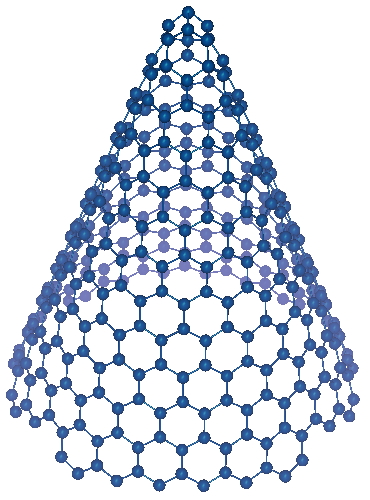
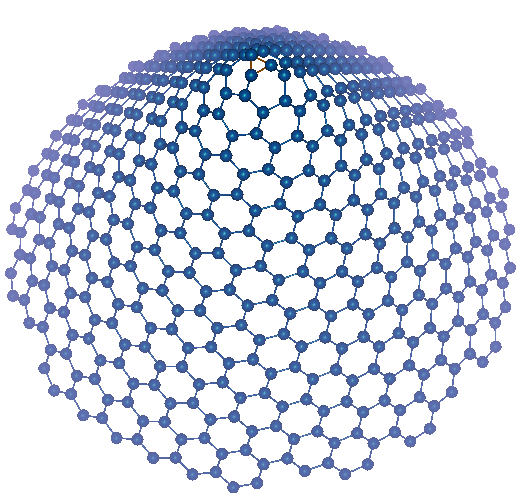
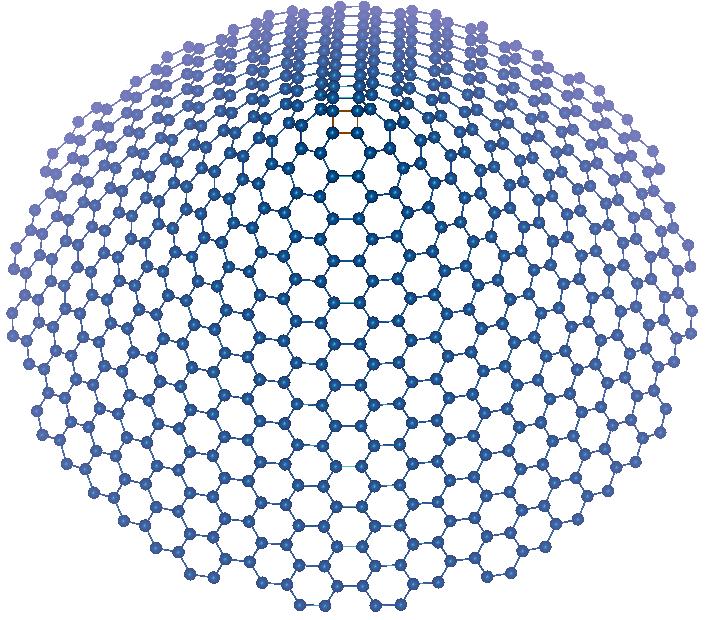
Thus, one can distinguish five different non-chiral versions of cones
(actually, six, if we consider the graphene cluster as a cone
with the apex equal to 180°). Obviously, these cones half-apex will be
determined by the formula:
$$
\Theta (p) = {\rm arcsin} \left( \frac{p}{6} \right)
$$
where p is the order of the cone's rotation axis. Thus, all
non-chiral nanocone modifications correspond to apex angles α=19.2°;
38.9°; 60.0°; 83.6°; 112.9° and 180°.
If we take into consideration also the chiral cones, the number of
possible angles is huge, though some angles are not allowed.
 |
 |
 |
| p=1; α=19.2° |
p=2; α=38.9° |
p=3; α=60.0° |
 |
 |
| p=4; α=83.6° |
p=5; α=112.9° |




